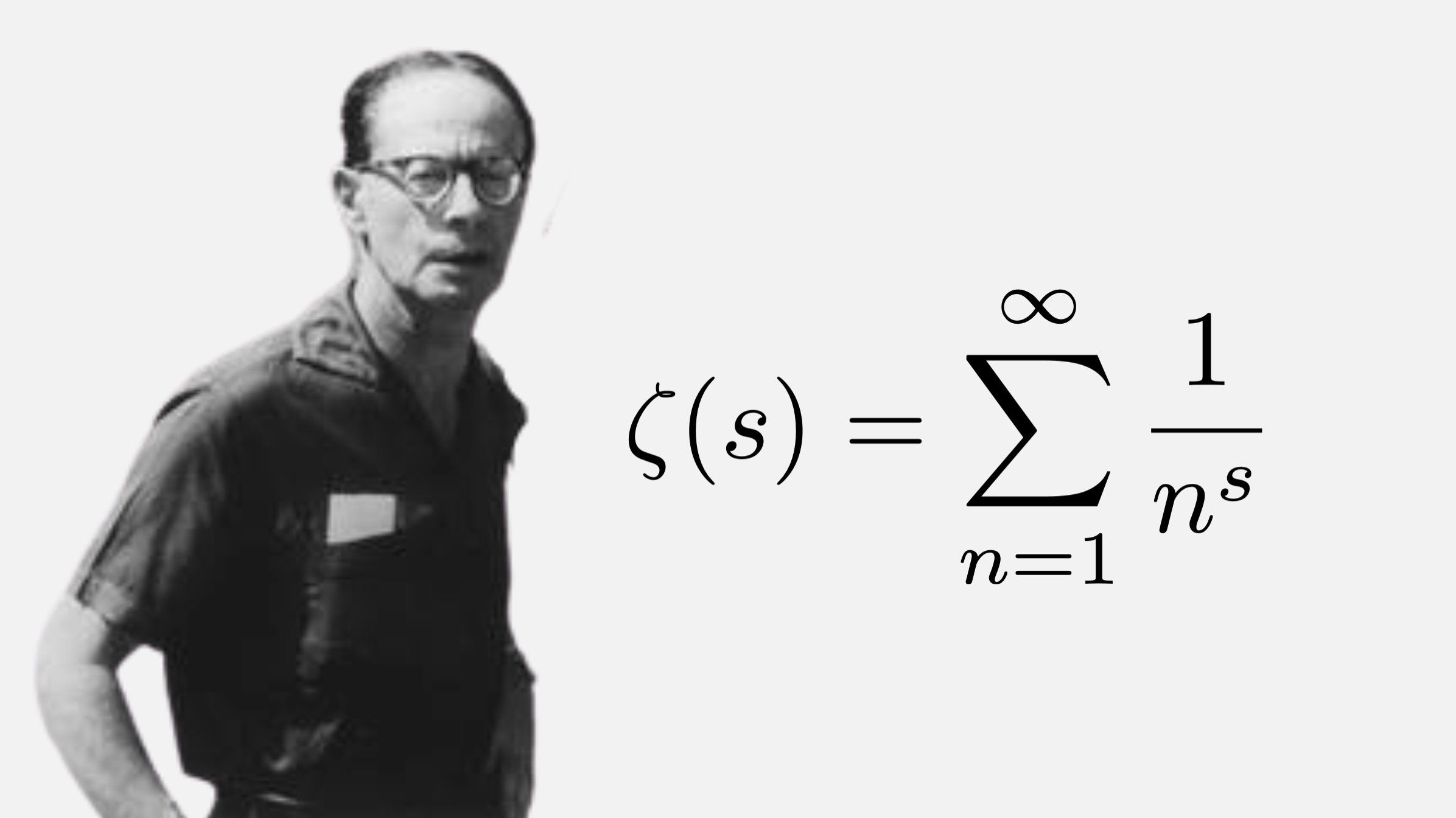有限域曲線的黎曼假設
1940 年,法國數學家安德烈·威爾(André Weil)因未報到而入獄。在魯昂(Rouen)監獄服刑六個月期間,他證明了有限域曲線的黎曼假設(The Riemann hypothesis for curves over finite fields)。
Riemann 的 zeta 函數:
\(\zeta(s) = \sum_{n=1}^{\infty} \frac{1}{n^s}\)
這個式子只在 Re s > 1 才成立,但 Riemann 把它推廣到了複數平面。
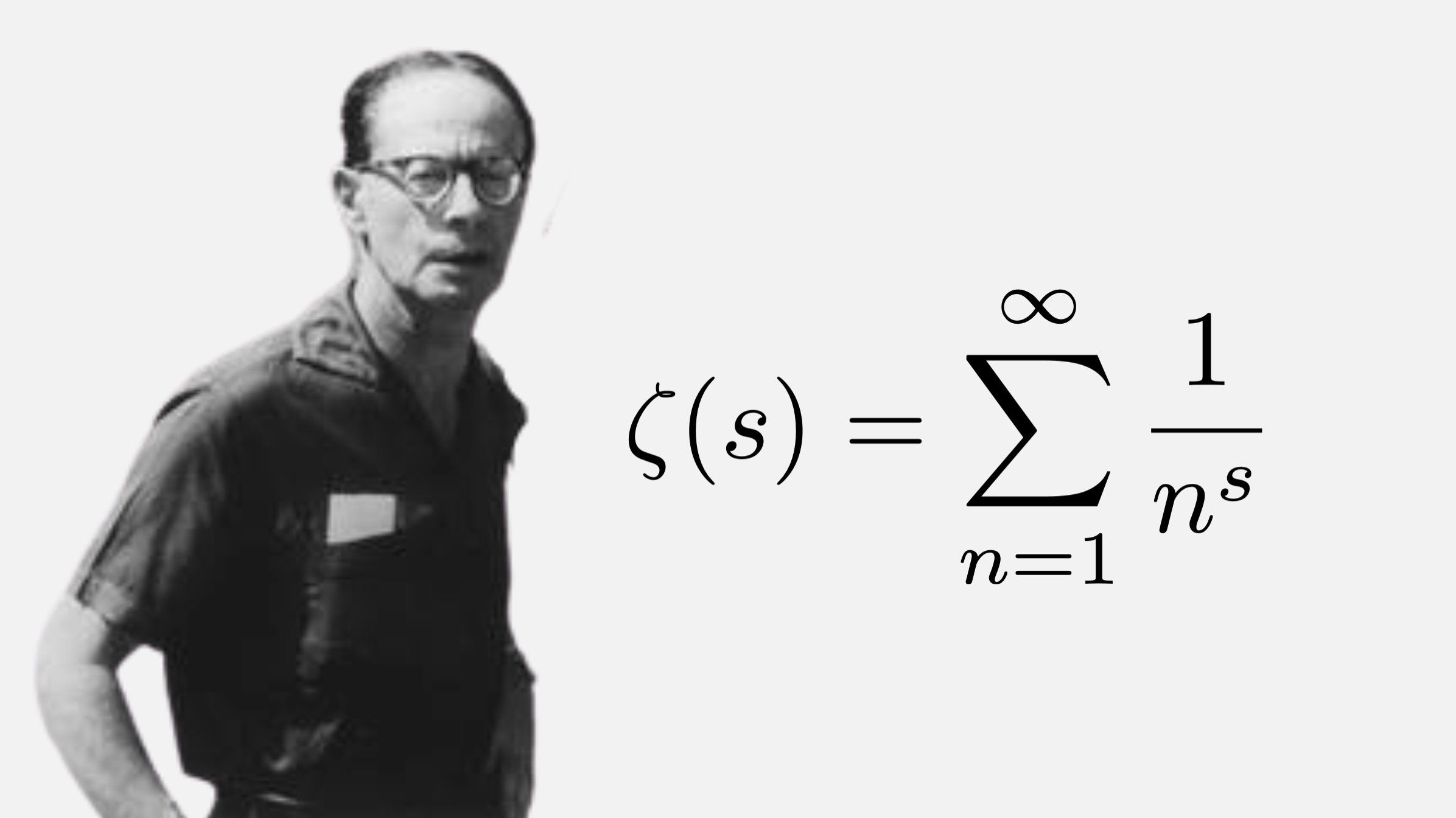

1940 年,法國數學家安德烈·威爾(André Weil)因未報到而入獄。在魯昂(Rouen)監獄服刑六個月期間,他證明了有限域曲線的黎曼假設(The Riemann hypothesis for curves over finite fields)。
Riemann 的 zeta 函數:
這個式子只在 Re s > 1 才成立,但 Riemann 把它推廣到了複數平面。